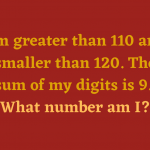The true sign of intelligence is not knowledge but imagination.These 10 Old Equations Proved Impossible To Solve
Quiz: 10 Old Equations Proved Impossible To Solve
Mathematics has always been a fascinating subject for many people. It is a subject that requires a lot of patience, hard work, and dedication. One of the most interesting aspects of mathematics is the equations that have been proved impossible to solve. These equations have been a mystery for mathematicians for centuries, and they continue to be a challenge even today.
In this quiz, we will explore 10 old equations that have been proved impossible to solve. These equations have been a source of frustration for mathematicians for many years, and they have tried various methods to solve them. However, despite their best efforts, these equations remain unsolved.
The quiz will test your knowledge of these equations and their history. You will be asked to identify the equations, their properties, and the attempts made to solve them. You will also be asked to explain why these equations are important and what impact they have had on the field of mathematics.
Whether you are a student of mathematics or just someone who is interested in the subject, this quiz is sure to challenge you and expand your knowledge. So, get ready to test your skills and see how much you know about these 10 old equations that have proved impossible to solve.
FAQ 1: What are the 10 old equations that are impossible to solve?
The 10 old equations that are impossible to solve are:
- Quintic equation
- General polynomial equation of degree 5 or higher
- Trisecting an angle
- Doubling the cube
- Squaring the circle
- Constructing a regular heptagon
- Constructing a regular nonagon
- Constructing a regular hendecagon
- Constructing a regular dodecagon
- Constructing a regular 257-gon
FAQ 2: Why are these equations impossible to solve?
These equations are impossible to solve because they cannot be solved using algebraic operations and radicals. In other words, there is no formula that can express the solutions of these equations in terms of the coefficients of the equation using only addition, subtraction, multiplication, division, and taking roots.
FAQ 3: What is the significance of these unsolvable equations?
These unsolvable equations have been a subject of fascination and study for centuries. They have led to the development of new branches of mathematics, such as Galois theory, which studies the symmetries of equations and their solutions. They have also inspired mathematicians to search for new methods of solving equations, leading to breakthroughs in other areas of mathematics and science.
